The focus of this project lays on reflection length in non-affine infinite Coxeter groups. Coxeter groups are abstract reflection groups, which can be classified roughly by the type of space they act on. Each element of the group acts by applying a finite sequences of reflections in the according space. For a fixed element this sequence doesn't have to be unique. The minimal number of reflections that suffices to represent a certain group element is called the reflection length of this element. One reason why the reflection length is well understood in the spherical and affine case is that it is bounded in this cases. On the other hand a result by Duszenko states the opposite for non-affine infinite (hyperbolic) Coxeter groups. This is one out of many examples where properties of Coxeter groups are unclear in the hyperbolic case, that are clear in the former settings.

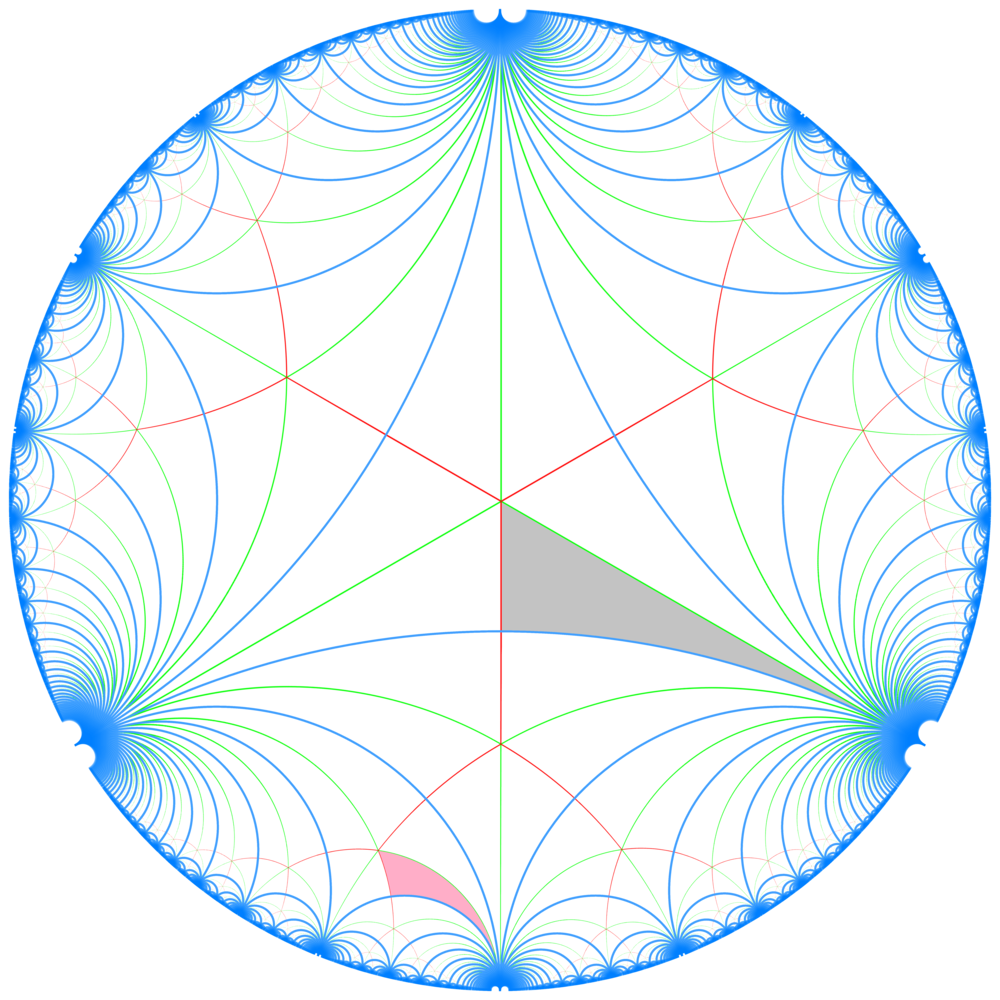
By using this duality of rich group theory for coxeter groups and the geometric realisation, we study the asymptotic behaviour of the reflection length. The objective of this project is to find repetitive patterns and prove structural results about the reflection length function in the hyperbolic setting: Even though the reflection length is unbounded, it already seems difficult not only to cumpute it but also to find elements with great reflection length in hyperbolic Coxeter groups. /